BBD使用エフェクタについて
はじめに、ここではBBD自体の原理についての説明は他に譲って、
BBDを使用した揺れモノエフェクタについての動作機序を重点的に
説明したいと思います。
BBDを使用したエフェクタの場合、
BBDに送るクロックでバッファの出し入れを制御するわけですが、
クロックを一定とした場合には、単純にバッファに信号が入ってから
出るまでの時間(=バッファのステップ÷クロック周波数)だけ
入力信号が遅延して出力されるディレイとして働きます。
このバッファのステップについてはBBDの品種によって異なります。例えば、
MN3005/3205やSAD4096は4096ステップ
MN3008/3208は2048ステップ
MN3007/3207は1024ステップ
MN3010やSAD1024は512ステップ×2系統
このときクロックの速さを変化させると、出力される音程も変化します。
例えばアナログディレイの場合、ディレイタイムのツマミでクロックの速さを設定しているので、ディレイ作動中にこのツマミをひねると、実際に音程が変化する様子が容易に確認できます。
とはいえ、無限にクロックを速く/遅く変化させ続けるというのも無理な話(説明については下記<クロックの速度変化と音程との関係>参照)なので、次に、LFOによりクロックの速さを(適正なクロックの範囲で)周期的に変える(FM変調)ことが考えられるようになったのだと推測します。
それがコーラス/フランジャー(あとBossVB-2Vibrato等)と呼ばれるエフェクタです。
コーラスとフランジャーの違いは本質的にはあまりなく、
コーラスにおけるディレイタイムが30〜60ms程度なのに対して、フランジャーのディレイタイムは0.5〜10ms程度であること、フランジャーにはコーラスにはあまり見られないフィードバックの機能がついていることぐらいになります。
なお、一部のフランジャーでは、ディレイタイムを最小 かつ LFOの振幅を最大にした場合、LFO波形の頭でBBDの動作不良が認められる(ノイズが出力される)ことがあります。
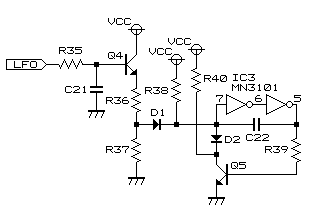
実際のコーラスの回路において、BBDのクロックをLFOでモジュレートする方法は歴史的には幾通りかあるようですが、ここではBOSS CE-2で初めて採用されて現在ではコーラス回路のデファクトスタンダードになった(ような感のある)"双曲線VCO"回路(上図)の場合を中心に、LFOの波形と音程変化の関係を考えたいと思います。
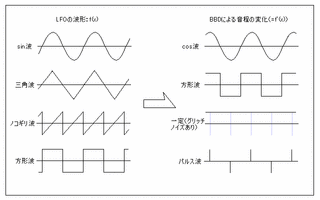
双曲線VCO回路において上図のようにLFOの波形(=クロック周波数の変化)を
sin波にすると音程の変化はcos波になり(→音が揺れるコーラス)、
三角波にすると方形波に(→音の揺れがないコーラス)、
ノコギリ波にするとグリッチを含んだ直線に(→(グリッチの大きな)ピッチシフタ)、
方形波にするとパルス波(→(グリッチの大きな)ディレイ。意味なし!)となります。
以上より、クロックの速さと音程の変化との間には、微分(差分?)の関係が認められる事となります。(この辺もう少し突っ込んだ議論は、下記<双曲線VCO回路におけるLFOの波形と音程変化の関係>参照)
ちなみにBossのコーラスは、LFOの波形をきれいな三角波にすることで、BBDの出力の音程が(コーラスの出音も)揺れるのを防いでいるとの話です。
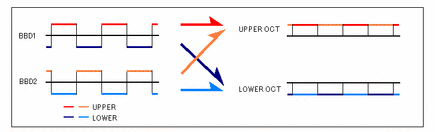
ここで、2系統のBBDを並列に用意してそれぞれに位相の反対な三角波を送った場合、それぞれのBBDの入力が同じならば、上図のように出力の音程変化は互い違いの方形波になりますが、それら出力をミックスした場合、結果的に一定の音程で上下にデチューンされたふたつの音になります。これがいわゆるディメンションの原理です。
またデチューンされた音の片方だけ取り出せば、上のノコギリ波の場合よりはグリッチの少ないアナログハーモナイザになります。
<クロックの速度変化と音程との関係>
クロックの初速度をf0(Hz)とすると、1クロック(1ステップ)あたりかかる時間は1/f0秒になります。使用するBBDのステップ数をSとすると、音程がh倍になるためには、Sステップ後にクロックがh倍(Sステップ後の1クロックあたり時間は1/h倍)になっている必要があります。
よって、1ステップごとに1クロックあたり時間は1/h1/S倍になる計算になります。
ここで、トータル経過時間Tと、時間Tだけ経過した時の周波数f(Hz)を考えます。
T=1/f0+1/h1/S・1/f0+1/h2/S・1/f0+・・・+1/h(n-1)/S・1/f0
=(1-1/hn/S)/(1-1/h1/S)・1/f0
(等比級数の公式を使用)
このとき、1/f=1/f0・1/hn/Sなので、
∴T=1/(1-1/h1/S)・1/f0-(1/hn/S)/(1-1/h1/S)・1/f0
=(1/f0-1/f)/(1-1/h1/S)
f→∞のとき、T→(1/f0)/(1-1/h1/S)となり、有限の値に収束してしまいます。つまり、ずっと周波数をh倍し続けるという方法によるピッチシフトは、原理的に有限時間しか持続しないことになります。
(逆に、ずっと周波数を1/h倍し続ける方法によるピッチシフトは、いずれ入力信号がBBDを通り抜ける時間が∞になってしまう)
例えば、初速度f0=10kHz,音程2倍、BBDステップ数1024のとき、
T=(1/f0-1/f)/(1-1/h1/S)=0.147(秒)以上ピッチシフトを持続させることは理論上できません。
まあ、BBDのクロック周波数にも上限/下限周波数があるので、無限に周波数を上げ続ける(下げ続ける)ことなどもちろんできるわけがないのですが。
<双曲線VCO回路におけるLFOの波形と音程変化の関係>

LFOによるCVはQ4でバッファリングされ、電流逆流防止用のダイオードD1を経てインバータの入力(MN3101の7ピン)の下限電位を決定します。電源電圧とこのCVによる下限電位との電位差 および R38で決まる電流が、C22に充電されます。なお、この回路のクロックジェネレータMN3101の縦列インバータ(シュミットトリガ)とC22は、リセット型VCOを構成しています。
流れ込んだ電流がC22に充電されることにより、インバータ入力の電圧が上がります。この電圧がシュミットトリガのしきい値を超えると、出力(MN3101の5ピン)がHの状態になります。出力がONになると、Q5がONしてコレクタ電位が下がり、D2が導通してC22に溜まった電荷を放出して、結果的にインバータ入力が下限電位にリセットされ、出力もLの状態にリセットされます。
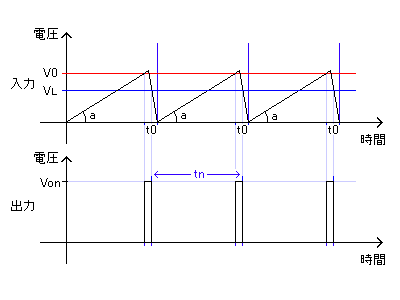
この一連の動作におけるインバータの入力(MN3101の7ピン)の状態を図示したのが上図のグラフ上側です。aの傾きは単位時間あたりの充電量で、電源電圧とR38で発生する電流 および C22により決まります。(もちろんインバータ入力の電位が上がってくるとR38の両端にかかる電圧が下がるため、aの傾きもなまってくるはずですが、電源電圧がしきい値に対して十分高いならば、aはほぼ一定であると考えてしまってもよいように思います。)
充電により電圧がONしきい値V0を超えると、シュミットトリガの反応時間だけ遅れてQ5のベースに電圧がかかり、その後Q5のON時間だけ遅れてC22が放電されます。C22の放電により、入力の電圧がOFFしきい値を下回ると、出力は0Vにリセットされます。この一連の動作におけるシュミットトリガ出力は、グラフ下側のようなt0の幅をもったパルス波になりますが、外部からのCVがない場合は、上記の要因のみでこのパルス間隔tn(発振周波数の逆数)が決まります。
tn=V0/a+t0
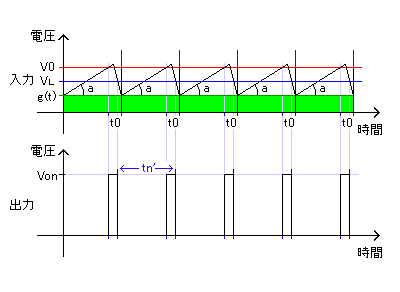
外部からのCVがある場合、 発振周波数f0≫LFOの周波数 ならば1サイクルを考えた時のCVの電位はほぼ一定と考えられます(上図の緑色の部分)。また、電源電圧≫CVの変化量 ならば、電源電圧とこのCVによりゲタをはかされた下限電位との電位差 および R38で決まる電流 ならびに 単位時間あたりの充電量aもほぼ一定と考えることができます。この場合において、LFOの波形をg(t)と置いてパルス間隔tn'を考えると、以下のようになります。
tn'=(V0-g(t))/a+t0
この時、BBDの入出力における周波数変化h(t) および 音程変化s(t)を考えると、
h(t)=fn[0]/fn[-1]=tn[-1]/tn[0]
s(t)=log(h(t))=log(tn[-1]/tn[0])
fn[0]:現在の周波数
fn[-1]:現在よりmステップ前の周波数
tn[0]:現在のパルス間隔
tn[-1]:現在よりmステップ前のパルス間隔
(m:BBDのステップ数)
ここで tn'=(V0-g(t))/a+t0 より、
tn[0]=(V0-g(t))/a+t0
tn[-1]=(V0-g(t-tn[0]))/a+t0
(t-tn[0]:現在よりmステップ前の時間)
tn[0]-tn[-1]=(V0-g(t))/a+t0-((V0-g(t-tn[0]))/a+t0)
=(-g(t)+g(t-tn[0]))/a
a(tn[0]-tn[-1])=-g(t)+g(t-tn[0])
a(tn[-1]-tn[0])=g(t)-g(t-tn[0])
∴a(tn[-1]/tn[0]-1)=(g(t)-g(t-tn[0]))/tn[0]
このとき右辺の式は、tn[0]が限りなく0に近いとすると、導関数g'(t)で近似できる。
a(tn[-1]/tn[0]-1)=(g(t)-g(t-tn[0]))/tn[0]=g'(t)
tn[-1]/tn[0]-1=g'(t)/a
tn[-1]/tn[0]=g'(t)/a+1
∴h(t)=tn[-1]/tn[0]=g'(t)/a+1
以上より、BBDのクロック周波数≫LFOの周波数 で、BBDのステップ数がそんなに長くなくて、かつ LFOの振幅がONしきい値に対して大き過ぎない場合は、fn[0]とfn[-1]の差分によりきちんとLFOの波形の接線が近似できるために、ほぼ微分の関係と捉えても問題ない状況になるのだと思います。
なお音程変化s(t)は、以下のようになります。
s(t)=log(h(t))=log(g'(t)/a+1)=log(g'(t)+a)-log(a)
∴s(t)=log(g'(t)+a)-log(a)
(この項終わり)