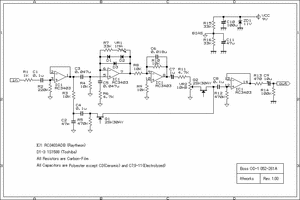
Boss OD-1(QuadVersion)
<OD-1A>
ロットNO.:6400-6500
PCBのマーキング:"052-281A"
スイッチ:透明
ネジ:銀ネジ
OP-AMP:RC3403ADB
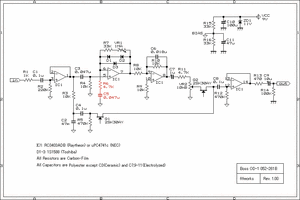
<OD-1B>
ロットNO.:6600-8800
PCBのマーキング:"052-281B"
スイッチ:8400まで透明,8600から黒(8500は未確認)
ネジ:銀ネジ
OP-AMP:8300までRC3403ADB,8400はRC3403ADBとμPC4741両方,おそらく8500からμPC4741C(ex. 8700)
OD-1AとOD-1Bとの回路上の違いは、図中赤で示した抵抗R6とコンデンサC5の
つなぎ順の違いのみ。微妙にOD-1Aの回路の方が発振しやすそうな気はするが、
実はわたしにはあまり本質的な違いはわかっていない。(書きかけ)
ちなみに、ロットNO.8900からはデュアルOP-AMPを使った別回路になる。
このタイプのPCBは"052-281D"になっているので、おそらく"052-281C"という
時期はなかったものと思われる。
(QUAD OP-AMP VersionをLED常時点灯化対応した基盤のためにリザーブされていたのかも??)
ロットNO.:8900-(少なくとも6桁になるまで)
PCBのマーキング:"052-281D"
スイッチ:黒
ネジ:0300まで銀ネジ,0500以降は黒ネジ(0400もSD-1の類推からおそらく黒ネジ)
OP-AMP:NJM4558D(JRC)(ex.9900)
(ただし9300,0300はμPC4558C(NEC),0000はTL4558P(TexasInst.))
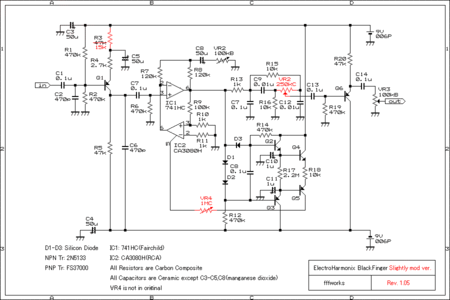
ElectroHarmonix Blackfinger
<Slightly MOD Versionの説明>
アタックをコントロールするため、上図のようにIabcをコントロールする可変抵抗をつけてみました。
(ROSS CompressorやBOSS CS-2あたりにも同様の可変抵抗がついています)
わたしは手持ちの抵抗(2MΩCカーブ)をあつらえましたが、値に特に意味はないです。
でもCカーブにしておいたほうが設定がしやすいです。
この抵抗を絞り切ればオリジナルと同じ設定になるので、実機の設定を保ちつつ
より楽器として使いやすい設定もできる、という寸法です。
入力の楽器によっても微妙に変わるとは思いますが、わたしは、この可変抵抗を
12時の位置付近に設定して使うことが多いです。
トーン回路のVR2については、TSC in the Web でシミュレートしながら決めました。
よりハイを強調したセッティングも可能となるので、250kΩとした方がコンプに合うような気がしています。
ElectroHarmonix Blackfinger
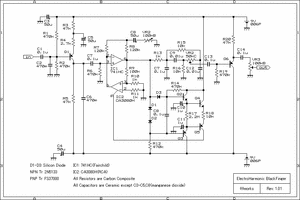
<回路全体の構成>
入力信号は、Q1で入力を増幅した後(交流的にはR5/R4倍(約17.4倍))、IC1/IC2のVCAユニット、BigMuffタイプのトーン回路を経てQ6の出力バッファへ流れます。VCAユニットの後ろに信号レベル検出回路がついているフィードバック型の構成のコンプレッサーになります。
<信号レベル検出回路について>
VCAユニット後ろにつながる検出回路は、D1-D2方面とD3方面に分かれます。この辺何故非対称なのかは不明です。ダイオードが2つだと反応し過ぎ・4つだと反応しなさ過ぎということで現物合わせ的に決定されたのかもしれません。
D1-D2,Q3により振幅の下側が増幅され、C10で平滑化されてQ5に至ります。また、振幅の上側についてはD3,Q2により増幅され、C11で平滑化されてQ4に至ります。そして、Q4とQ5にはさまれたR18にかかる電圧と抵抗値により決まる電流がQ5のコレクタから放出され(Q5のベース電流は比較的小さいので無視)、OTA(OperetionalTransconductanceAmplifier:トランスコンダクタンスアンプ)のIabc(アンプバイアス電流=OTAのトランスコンダクタンスを制御する電流)となります。
ちなみに、R18の両端には電源電圧(9V×2=18V)を超える電圧がかかることはないので、Iabcは最大でも18V÷10k=1.8mAとなり、絶対定格(2mA:HarrisCA3080データシートより)を超えることはありません。
この際、D1-D3の順方向電圧降下およびQ2-Q5のVbeより、入力がない場合はR18には電圧がかかりません。理由は、入力がゼロの場合、Q2,Q3のベース・エミッタ間電圧VbeとD3,D2の順方向電圧降下が概ね相殺され、Q4,Q5において、それぞれのVbeの合計(=R17にかかる電位差)がD2の順方向電圧降下分程度しか確保できないためOFFになり、コレクタ→エミッタに電流が流れないことによります。
信号が検出回路に入力された場合、前述のように振幅の上側はD3,Q2,C11,Q4により、振幅の下側はD1-D2,Q3,C10,Q5により検出→平滑化→増幅されてR18の両端電圧になります。その際波形が対称ならば、D2ひとつ分のオフセットのため、Q4のエミッタ−アース間電位 > アース−Q5のエミッタ間電位となります。結果として、検出回路全体では上下非対称の動作をすることになります。
C8により検出回路への入力のうち高周波成分がカットされます。カットオフ周波数は、D1-D3の存在により見えにくくなっていますが、概ねC8およびIC1/IC2によるVCAユニットの出力インピーダンスにより決まるのではないかと思います。
また平滑化の時定数は、C10,C11およびR17によって決定されるものと思われます。
(T=C10×R17/2ぐらいかな???)
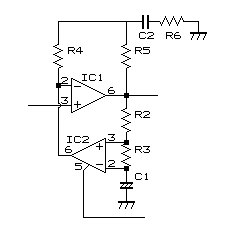
<VCAユニットについて>
特徴としては、OTA(IC2)をそのまま信号経路に使わないで、IC1のフィードバック経路に使っている点があります。VCAは反転入力と非反転入力の差動入力電圧をなるべく少なくしないと出力が歪んでしまうため(せいぜい±5-10mV程度。計算は下記<差動入力電圧範囲の試算>参照)、直接信号経路に使った場合は、信号を一度十分アッテネートした後で再度増幅する必要があります。
この回路のようにOTAをフィードバック経路に使うことで、Q1を出た信号をアッテネートすることなくIC1にぶち込むことができます。しかしフィードバック経路にあっても、結局はR9/R10によりアッテネートしないとIC2の入力が飽和してしまいますが。さらにR9/R10に対してR11をセットしてなるべくオフセット等が少なくなるようにしているようです。
このアイデアがどの程度有効かについては、下記<BlackFinger型VCAユニットの検証>で計算してみます。
そういえば、IC2を無視するとIC1周りはT型帰還回路になっていることに気づきます。この形の回路は昔のアンプの初段増幅で使われているのを見た事があります。参考文献1にあるT型帰還回路におけるY-Δ変換を行って計算すると、交流ゲイン(つまりC8を無視)は120k/VR2倍(1.2〜オープンループゲイン倍)となります(実際には先ほど無視したIC2(OTA)もフィードバックに関与するので、本当にオープンループゲイン倍になるわけではない)。
下記<BlackFinger型VCAユニットの検証>での計算結果から考えるに、T型帰還回路とOTAのフィードバック回路を組み合わせることにより、巧妙にダイナミックレンジを稼ぎつつ歪みを抑え、かつソフトニーなコンプレッション特性を得ているようです。
ちなみに、もう少し後の機種では、IC2の非反転入力と反転入力を比較的低い値の抵抗でつなぎ、さらに反転入力とアースの間に大容量のコンデンサ(数〜数十μF程度)をつなぐような回路も採用されています。
<欠点>
実はこのBlackfinger、6弦を思いっきり弾いたりコードを掻き鳴らしたりすると音が消えます。
そういう「仕様」なのでしょうがないといえばしょうがないのですが、この現象は、Q1のバイアスが正電源側に寄りすぎているかエミッタ抵抗が大きすぎるかのためにコレクタ電流が十分に取れず、大きい入力信号に対して波形の片側がクリップしてしまう(飽和領域での動作となる)ことが原因で起こっているようです。この辺りの状況については下記<Q1の動作検証>に詳しく書きます。
(r0r0さんご教示ありがとうございました)
また、他のコンプのように電流を供給源Q5とOTAの5ピンとの間に可変抵抗をつなぐことで、Iabcの変化範囲を適度にコントロールできるようになります。
上記の改善策については、MODの項をご参照ください。
<CA3080の回路解析>
HarrisCA3080データシート中の Schematic Diagramより、D1,Q3はカレントミラー回路になっているので、ID1=Q3のコレクタ電流IC3と考えることができます。(ダイオードの飽和電流は、参考文献2によると10-16から10-10Aとのことなので、ここでは無視する)
よって、Q3のhFEをhFE3とすると、Iabc(アンプバイアス電流:Amplifier Bias Current)は、
Iabc=ID1+IB3
=IC3+IC3/hFE3
={(hFE3+1)/hFE3}・IC3
トランジスタのhFEは通常100程度はあるので、(hFE3+1)/hFE3≒1と考えることができます。
∴Iabc≒IC3・・・(1)
Q1のコレクタ電流IC1およびQ2のコレクタ電流IC2とIC3の関係は、Q1とQ2のhFEをそれぞれhFE1, hFE2とすると、
IC3={(hFE1+1)/hFE1}・IC1+{(hFE2+1)/hFE2}・IC2
例によってトランジスタのhFEは100程度なので、(hFE1+1)/hFE1≒1,(hFE2+1)/hFE2≒1と考えることにします。よって、
IC3≒IC1+IC2
上式および(1)の結果より、
∴Iabc≒IC1+IC2・・・(2)
よって、IabcはほぼIC1とIC2の合計に等しくなります。
この時、Q8,Q9がダーリントン接続なのでQ7,D3(多分D5の誤植),Q8,Q9は全体としてウイルソン型カレントミラー回路として働く(D4はQ8のE-B間保護用。通常は非導通)ため、結果として、Q8,Q9の出力電流=IC2 となります。
同様に、Q5,Q6がダーリントン接続なのでQ4,D3,Q5,Q6は全体としてウイルソン型カレントミラー回路として働きます(D2はQ5のE-B間保護用。通常は非導通)。ただし、このまま出力をつなぐと全波整流回路になってしまうので、この出力をさらにQ10,Q11,D6によるウイルソン型カレントミラー回路によって反転して出力しています。よって、Q10の出力電流=-IC1(極性が反対になっていることに注意)となります。
よって、IC全体の出力電流Ioutは、Q8,Q9の出力電流とQ10の出力電流の和に等しいので、
∴Iout=IC2-IC1・・・(3)
(2)および(3)より、出力電流IoutとIabcの関係は、以下のようであることがわかります。
|Iout|≦Iabc (等号はIC1もしくはIC2のいずれかがゼロの時に成立する)
つまり、Ioutの最大振幅はIabcによって決まる、ということです。
<差動入力電圧範囲の試算>
差動入力回路におけるペアトランジスタQ1,Q2のコレクタ電流IC1,IC2は、参考文献3:pp39-40にある通り、以下のようになります。参考文献3中のVID,IC5はそれぞれVin,IC3に対応します(IC1,IC2はそのまま)。
IC1=IC3/2・{1-tanh(x)}
IC2=IC3/2・{1+tanh(x)}
x=Vin/2VT
(VT:熱電圧 接合部温度T=300Kのとき25.85mVとなる)
上の式をグラフ化したのが下図です。
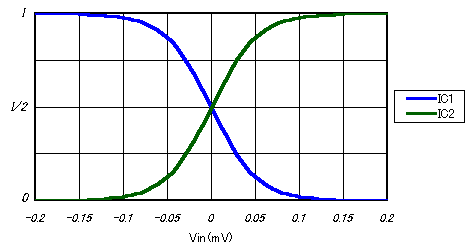
グラフより、差動入力電圧の絶対値が大きくなればなるほど入出力のリニアリティーが失われる(つまり歪みが増える)ことが直感的に見てとれます。(見てとってください)
次に、差動入力電圧がどれくらい大きくなるとどれくらい歪むのかを定量的に示してみます。
(1)および(3)の結果を考慮すると、出力電流Ioutは以下の通りになります。
Iout=IC2-IC1=IC3・tanh(Vin/2VT)
≒Iabc・tanh(Vin/2VT)
トランスコンダクタンスGmは、出力電流Ioutおよび差動入力電圧Vinを用いて以下の通り表すことができます。
Gm=dIout/dVin=dIout/dx・dx/dVin
dIout/dx=Iabc・1/cosh2(x)
dx/dVin=1/2VT
∴Gm=Iabc・1/cosh2(x)・1/2VT=Iabc/2VT・1/cosh2(Vin/2VT)
よって、原点(Vin=0)ではcosh(0)=1なので、Gm(0)=Iabc/2VT=19.38・Iabc(T=300Kのとき)となります。
この時、Gm(0)に対するGmの誤差を±a%以下にすることを考えてみると((100-a)%≦Gm/Gm(0)≦(100+a)%)、
Gm/Gm(0)=Iabc/2VT・1/cosh2(Vin/2VT)/(Iabc/2VT)=1/cosh2(Vin/2VT)
cosh(x)≧1より、1/cosh2(Vin/2VT)≦100%となり、Gm/Gm(0)は100%を上回ることはないので、下限(100-a)%だけ考えればよいことになります。
Gm/Gm(0)=1/cosh2(Vin/2VT)≦(100-a)%
1/(1-a/100)=cosh2(Vin/2VT)
Vin/2VT=arccosh((1-a/100)-1/2)
∴Vin=2VT・arccosh((1-a/100)-1/2)
上の式をもとにExcelで実際の値を計算してみました。
許容誤差aを1%すると、許容差動入力電圧範囲Vinは±5.187mVとなります。また、許容誤差aを5%すると、Vinは±11.759mVとなります。思った以上に狭くてびっくりです。
<BlackFinger型VCAユニットの検証>
まず、IC1周りはT型帰還回路となっているので、参考文献1にあるY-Δ変換を行ってπ型帰還回路に変換します。
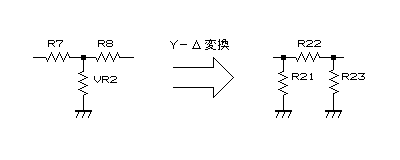
今回は交流特性のみ考えることにしてC8を無視すると、結果は以下のようになります。
R21=R7+2・VR2=120kΩ+2・VR2
R22=(R7・R8+R7・VR2+R8・VR2)/VR2=240kΩ+120kΩ2/VR2
R23=R8+2*VR2=120kΩ+2・VR2
IC1の出力電位をVout、OTA(IC2)の非反転入力の電位をVa、IC1の反転入力の電位をVinと置くと、VCAユニット全体の増幅率Avを求める式は以下のようになります。
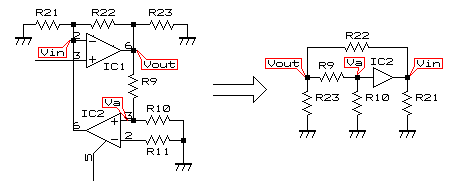
Va=R10/(R9+R10)・Vout=1/101・Vout
Ia=Va・Gm=Gm/101・Vout (Gm:OTA(IC2)のトランスコンダクタンス,Ia:OTAの出力電流)
Vin=If・R21+Ia・R21 (If:帰還抵抗R22を流れる電流)
Vout=If・(R22+R23)+Ia・R21
Av=Vout/Vin
以上の連立方程式を解くと、
Vout=If・(R22+R21)+Ia・R21=If・(R22+R21)+Ia・R21
Vout-Ia・R21=If・(R22+R21)
(1-(Gm・R21)/101)・Vout=If・(R22+R21)
∴If=(1-(Gm・R21)/101)/(R22+R21)・Vout
Vin=If・R21+Ia・R21=(If+Gm/101・Vout)・R21
=((1-(Gm・R21)/101)/(R22+R21)・Vout+Gm/101・Vout)・R21
=((1+(Gm・R22)/101)/(R22+R21))・R21・Vout
∴Av=Vout/Vin=(R22+R21)/((1+(Gm・R22)/101)・R21)
=101・(R22+R21)/((101+(Gm・R22))・R21)
この時、OTAをなるべく歪まないように使うことを考えます。<差動入力電圧範囲の試算>での結果からすると、OTAの入力が±5.187mV以内ならば(R9/R10により1/101にアッテネートされることを考えると、IC1の出力±5.187mV×101=±523.8mVならば)、OTAによる信号の歪みを1%以下に抑えることができるはずです。
このような条件でOTAを使用することにより、誤差1%の範囲内でGm≒Gm(0)=Iabc/2VT=19.38・Iabc(T=300Kのとき)と考えることができるようになります。
∴Av=101・(R22+R21)/((101+(19.38・Iabc・R22))・R21)
以上の結果を踏まえて、VR2を1kΩ,10kΩ,100kΩとしたときのIabcと出力の関係のグラフをExcelで書いてみました。簡単のため入力信号とIabcは比例することとしたので、出力はn×Iabc×Avの形になるはずです。今回はグラフの形を見たいだけなので、y軸をIabc×Avとして(nを省略して)グラフを書いてみました。
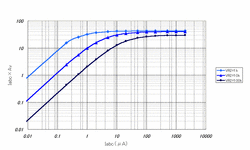
結果を見るに、入力に対してきれいにソフトニーな反応をしていることがわかります。また、VR2の抵抗値を小さくして行くと、徐々にコンプレッサーが深くかかるようになっています。
つまり、入力信号の絶対値にキレイに比例する電流を出力するような入力信号検出回路を使い、かつ通常の使用ではIC1の出力が±523.8mVを超えないように設定すれば、十分使いモノになりそうな予感です。
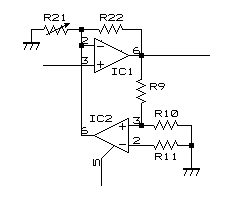
参考までに、T型帰還回路を採用せず、上図のようにR22を固定かつR21を可変して増幅率を調整するような回路構成とすると、以下のように、VR2の値を変えても圧縮の度合をコントロールすることができなくなります。(上:R22=500k,下:R22=∞Ω)
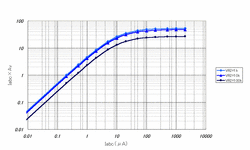
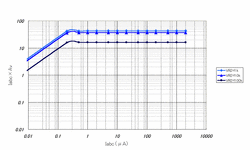
なるほどT型帰還回路を採用した意味がよくわかる結果となっているように思います。
<Q1の動作検証>
大きい信号を入力した際にQ1がどのように動作するかを考察したいと思います。
Q1のベース電流をIb, R1に流れる電流をIBIASとすると、
VCC=R1・IBIAS+R2・(Ib+IBIAS)
VCC=9V,R1=R2=470kΩ なので、
2・IBIAS+Ib=9V/470kΩ
IBIAS=4.5V/470kΩ-Ib≒9.574μA-Ib
Q1のコレクタ電流をIc,エミッタ電流をIeとすると、
Ic=hFE・Ib
Ie=Ic+Ib=(hFE+1)Ib
Q1のエミッタ電位をVe,ベース電位をVbとすると、
Ve+Vbe=Vb
オームの法則よりVe=(R3+R4)・Ie,Vb=R1・IBIASなので、
(R3+R4)・Ie+Vbe=R1・IBIAS
Ie/(hFE+1)=Ib,IBIAS=4.5V/470kΩ-IbよりVbe=0.6Vとすると、
(R3+R4)・(hFE+1)Ib+0.6V=470kΩ・(4.5V/470kΩ-Ib)
(R3+R4)・(hFE+1)Ib+0.6V=4.5V-470kΩ・Ib
(R3+R4)・(hFE+1)Ib+470kΩ・Ib=4.5V-0.6V
(R3+R4)Ie+470kΩ/(hFE+1)・Ie=3.9V
((R3+R4)+470kΩ/(hFE+1))・Ie=3.9V
∴Ie=3.9V/((R3+R4)+470kΩ/(hFE+1))
R3=47kΩ,R4=2.7kΩより、
Ie=3.9V/((47kΩ+2.7kΩ)+470kΩ/(hFE+1))
Ie=3.9V/((49.7kΩ)+470kΩ/(hFE+1))
hFE=100とすると、
Ie=3.9V/((49.7kΩ)+470kΩ/(100+1))
≒71.7μA
つまり、エミッタには最大でも71.7μAしか電流が流れない
→ (Ib≒Icと考えると)コレクタからは71.7μA×47kΩ≒3.37Vppしか電圧を取り出せない
ということになります。
(それ以上の電圧を無理やり取り出そうとするとトランジスタが飽和(クリップ)する)
Q1の交流増幅率はおおむねR5/R4≒17.4倍になりますので、ベースに加える信号が電圧ベースで3.37Vpp/17.4≒0.194Vppを超えると、波形の下側がクリップすることになります。
波形の片側がクリップした状態で信号レベル検出回路に信号が流れると、実際の出音とレベル検出回路における検出結果との間のバランスが崩れます。実際にはレベル検出回路が過剰反応を起こす(ほぼ波の大きい側のレベルで判定される)ことで、結果として音が消えるような現象が起きているようです。
レベル検出回路の検出結果(Iabc)を制御するような可変抵抗を入れることによってもある程度の操作性の向上は見込まれます(可変抵抗の位置によって音が消えないセッティングが可能になる)が、Q1で波形がクリップすることが音が消える根本的な原因なので、波形がクリップしない程度にQ1に流れる電流を増やすことこそが回路的に最も望ましい解決策となります。実装上はR3を15kΩ程度に減らしてやるとよいようです。
実装の詳細は、MODの項をご参照ください。
参考文献1:トランジスタ技術SPECIAL増刊:OPアンプによる実用回路設計(馬場 清太郎著、CQ出版社)
参考文献2:はじめてのトランジスタ回路設計(黒田 徹著、CQ出版社)
参考文献3:解析OPアンプ&トランジスタ活用(黒田 徹著、CQ出版社)
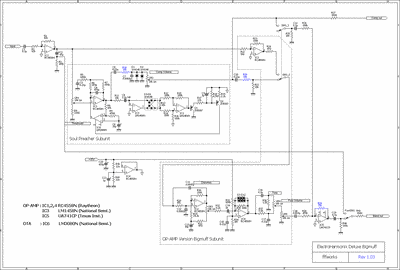
ElectroHarmonix Deluxe Bigmuff
<回路の概略説明、のようなもの:(回路図中青色の部分は2007/3/20修正)>
入力インピーダンスは~82k(R1そのもの)で、ギターを直接入力するには少し低いような気がします。
OP-AMP Version Bigmuff Subunitは、定数まで含めてオペアンプバージョンのBigmuffほとんどそのままです。R24,R29の定数とスイッチSW1_2が途中に入る点が違うといえば違いますが。トーン回路の定数がディスクリート版とかなり異なります。よりオーバードライブっぽい設定でしょうか。
このDeluxeBigmuffは、SoulPreacherとBigmuffを2in1にしたような構成のエフェクタです。(先日入手したSoulPreacherがほぼこの回路と同じ内容でした。そうなると、ディスクリート版SoulPreacherも試してみたくなります)
IC3周辺で絶対値化された信号をQ1,Q2でピークホールドしている感じでしょうか。ピークホールドの時定数はC9(1μF)とR18(4.7MΩ)決まると思いますが、Q2のベース電流がもれる分だけ短くなると思います。
VCA周辺の回路はBlackfingerと似ていますが、より進化しているように見えます。C6によりIC6の反転入力(2ピン)が交流的に接地され、R8とR9によって、差動入力電圧がIC1(1-3)の出力の1/100ぐらいに分圧されています。
この回路もQ2とIC6の5ピンとの間に可変抵抗をはさむことによってsensitivityを変えることができるはずです。ただ、実機でのコンプ感はBlackfingerよりおとなしいので、より微調整的に働くものと思われます。
純粋なコンプとして考えるとD1,D2の存在は微妙です(用途によってはLEDとかに置き換えたい気もします)。特にsensitivityの可変抵抗を増設した場合にはセッティングによっては歪み系の一種として考えたほうがいいのかも。
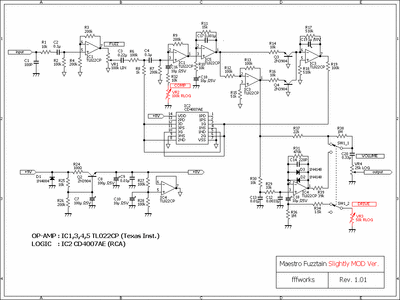
Maestro Fuzztain
http://www.dredgetone.com/Schematics/FuzzTain%20MZFT-272A.pdf
回路図まちがってます。サービスマニュアルなのに。
http://www.diystompboxes.com/smfforum/index.php?topic=46433.msg341311
ここの画像見る限りでは、R24は100kΩじゃなくて100Ωですね。
確かにここが100kΩだったら、電源の電圧降下がすごいことになります。
組み上げてから気づいたわけだが・・・。
ちなみにサービスマニュアル中のSN72L022Pというのは、TL022Pの旧型名です。
画像では76年製のTL022Pが使われてますね。
実は昔からFuzztainを作りたくて、ずいぶん前にSN72L022Pを無理やり探してもらって
大量に(50個)買ったのですが、TL022Pでいいんだったら、正直そんなに無理しなければ
よかったです。とてつもなく高かったし。
<回路の概略説明(になっているかどうか)>
IC3(1-3),Q3,Q4あたりが全波整流回路に、IC3(5-7)がピークホールド回路になるのだと思います。
元の信号がIC3(1-3)で反転されるためQ3,Q4のエミッタには互いに中点を基準として逆相の信号がかかり、Q3,Q4が交互にON/OFFすることによってその結果コレクタ側には全波整流された信号が現れるように思います。
(実際にはVBE分の不感帯が現れるような気もしなくはないですが)
ピークホールド回路の時定数はR17(510kΩ)とC19(1μF)で決まると思いますが、TL022CPなので電流がそれなりにもれるはずです。(計算上の時定数より短くなるはず)
ピークホールド回路の出力がCD4007に投入されてます。このCD4007はVoltageControlRegisterのような役割を求められているのでしょう。電圧と抵抗値のリニアリティーはどの程度あるのでしょうか?かなり気になります。
IC4(1-3)周辺はオーバードライブのような回路ですね。同時期に作られたMaestro FUZZ MFZ-1に類似しています。
(その前にR30,C13,R29,C12で構成されるパッシブフィルタがついてますが)
個人的にはIC3(1-3)で反転された出力をオーバードライブ回路の入力に使っているところに違和感を感じます。まあいいけど。
あと、IC1(1-3)とIC5(1-3)それぞれののオフセット×増幅率の分だけ全波整流の中点がずれるようにみえるけどいいのかな?
Maestro Fuzztain
<Slightly MOD Versionの説明>
SOFT → HARDを連続的に変えたかったので、モード切り替えはCOMP/FUZZの2通りとして、スイッチによる選択部分を可変抵抗に置き換えました。(上図中赤の部分)
OTA系コンプというかちょっとシンセっぽいです。ノイズもそんなにひどくないです。
CD4007の差し替えについては、フェイザーにおけるFETのばらつきぐらいの感じです。メーカーの違うヤツ同じヤツいろいろ何個か揃えておいて、気に入ったものを使えばいいと思います。
FUZZモードの方の音は、コンプ感の強い音から伸びる音までわりといろいろ出ます。COMP最大かつDriveをちょっと上げたぐらいのセッティングなど80年代を彷彿とさせます。メーカーも回路もかなり違いますが、DeluxeBigmuffのコンプ+ファズ直列モードにも似た味わいがあります。可変抵抗の部分を増やしたため、オリジナルにない中庸なセッティングも可能となり音色的には使いやすくなったと思います。
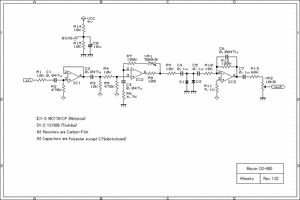
Maxon OD-880(Original)
1段目がボルテージフォロワでオペアンプ自体の入力インピーダンスが高く(741の場合、
オペアンプ自体の入力インピーダンスは無限大と言えるほど高くはない。下記参照)、
2段目の非反転増幅回路で約20〜120倍ほどゲインを稼いで(同時にC3,R6,R7+VR1
によるハイパスフィルタでローがカットされる)、D1,D2により±0.6Vの範囲でクリップ
され、続いて3段目の反転増幅回路で10倍に増幅された後(かつR10,R12,C6により
ハイカットされる)、最後にR13とVR2によりアッテネートされて出力される・・・ちょっと待った!
つーか、0.6V×10=6Vなので、D1,D2でクリップされても3段目で10倍に増幅され
ちゃあ電源電圧9V(つまり±4.5V)を遙かに超えてしまって、結局3段目のオペアンプの
最大出力振幅でさらにクリップされてしまう!!! なんてこったい。
この辺がオペアンプ使用初期のエフェクタ(確か1977〜78年ぐらいに発売開始のはず)
ゆえの結果オーライさというべきか。
何はともあれ、Charが使っていることで有名なこのOverdrive、出音のもっさり感の所以は
もちろん当時のローファイオペアンプ(MotorolaMC1741CP,1976年ごろ)による部分が
大きいようではある(自作してみてそう思った)のですが、もしかしたら加えてこのあたりの
設計の微妙さ加減(たぶん設計ミス)も影響しているのかもしれません。
<以下ちょっとだけ数値計算>
LM741,AD741等の入力インピーダンスRinは、カタログ値よりTyp.2MΩ
R2を含めたボルテージフォロワ全体の入力インピーダンスはRin//R2=2MΩ//470kΩ≒380kΩ
C2,R3によるハイパスフィルタの遮断周波数fc=1/2πCR=338.6Hz
C3,R6,R7+VR1による似非ハイパスフィルタの遮断周波数fc=1/2π(C3)(R6)=720.5Hz
R10,R12,C6による似非積分回路(≒ローパスフィルタ)の遮断周波数fc≒1/2π(C6)(R12)
=3386Hz
C4//C5,R10あたりの時定数もC2,R3あたりと同程度には効きそうなんですが、
D1,D2の存在のため線形計算が難しいので省略。
<以下は全体に対する影響が僅少のため無視>
C1,Rinによるハイパスフィルタの遮断周波数fc=1/2πCR=8.9Hz
C7,R13+VR2によるハイパスフィルタの遮断周波数fc≒1/2πC7(R13+VR2)=20.4Hz
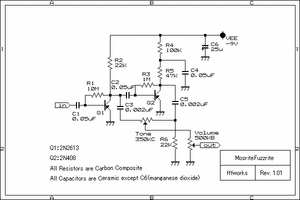
Mosrite Fuzzrite(GermaTr Ver.)
R1の10MΩですが・・・間違ってません。ゲルマの場合これでも動きます。まあこんなに高抵抗じゃあつながっていないのと同じような気もしますが。
理由としては、Q1自身の(コレクターエミッタ間の)漏れ電流により、ベースの電位が多少コレクタ側に引っ張られる(詳細はFuzzface概論1(ゲルマTrの特性)参照)のと、ゲルマTrのベースーエミッタ間電圧の低さ(おおむね0.06〜0.2V)とがあります。
その他はそんなにわかりにくい構成にはなってないと思います(単純な1段増幅回路×2をカップリングコンデンサでつないだだけ)。C4の付き方がちょっとトリッキーな気がしますが。R6の存在も微妙かな???
Toneによって、1段目のOUTと2段目のOUTのミックス量を可変できるようになっています。個人的には2段目のOUTをほんの少しブレンドしたぐらいのギターの持ち味を殺さない感じが一番好きです。
ちなみに、ここの抵抗値(350kΩ)は実測です。こんな値(しかもCカーブ)売っている訳ないので入手可能な値でいろいろ試してみたのですが、これが1MΩでも250kΩでも出音の雰囲気が違ってしまいました。
Q1のトランジスタの選別は結構シビアです。hFE90〜120ぐらいで漏れ電流が100μAぐらいのやつがベストです。てゆーか漏れ電流があまり多いと(>400μA)、R2による電圧降下によりコレクターエミッタ間電位が飽和します。ゲルマの場合、温度変化による特性の変化がひどいので、この辺それなりに余裕をもって対処した方が安全な気がします。
<オリジナル機のデータ>
Q1:2N2613 Q2:2N408
抵抗:CarbonComposite(Allen-Bradley??)
コンデンサ:Ceramic, Manganese dioxide
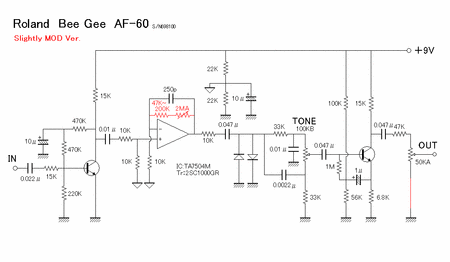
Roland BeeGee
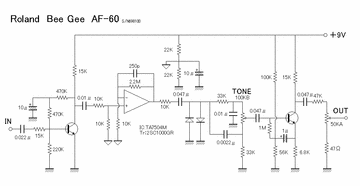
TA7504Mというのは、東芝の741互換のIC(CANタイプ)です。
1段目および最終段のトランジスタまわりの回路があまり見ない形ですが、それ以外はオーソドックスな回路構成だと思います。
1段目の回路ですが、電解コンデンサ10μFにより470kΩ×2の中点が交流的に接地されていますので、ベースのバイアスは安定化されますが、コレクタ→ベース間の負帰還は行われません。交流的に負帰還がかからないので、増幅率はオープンループゲイン倍(?)になります。
ただ、所詮トランジスタ1段なので裸の増幅率といえどもあまり高くはありません。この回路の場合を計算してみると(詳細は、下記<1段目トランジスタ回路の増幅率について>参照)、概ね95倍程度になります。
この辺、ファズなのでゲインをなるべく大きく、歪みは別に減らさなくてもいいや、という方針で回路設計されたのかな、という気がします。
トーンはいわゆるBigMuff型になっています。オペアンプ段での過激な増幅(増幅率:(2.2M+10k)/10k=221倍!)と相俟って、この辺がBeeGeeのFuzzたる所以になっているようです。
ちなみに、回路図を見てもわかるようにオリジナル機ではオペアンプ段のゲインが固定になっています。もしゲインを可変にしたい場合は、MODの項に示すようにオペアンプの帰還の2.2Mを可変にすることをおすすめします。
(反転入力からバイアスにつながる10kに2Mの可変抵抗を足してみたりもしたのですが、ゲインを下げた時の音があまり使いモノにならなかった。帰還抵抗が大き過ぎて入力バイアス電流が確保できなかったものと思われる)
2段目の回路について、電解コンデンサ1μFにより入力にブートストラップがかかっているため
(詳細は、下記<2段目トランジスタ回路の増幅率および入力インピーダンスについて>参照)、入力インピーダンスが1.7Mと高くなります。この場所で入力インピーダンスを稼いでもそんなに意味があるような気はしませんが・・・。増幅率は-Rc/Reのレベル(-2.5倍)とあまり高くはなく、この段ではゲインを稼いでいないことがわかります。
<1段目トランジスタ回路の増幅率について>
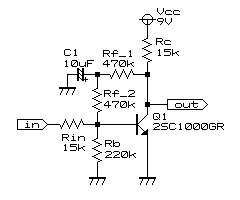
vout=Rc'・(-ic)=-Rc'・hfe・ib
vin=(Rin+hie')/hie'・hie'・ib=(Rin+hie')・ib
Rc'=Rc・Rf_1/(Rc+Rf_1)
hie'=hie・Rb・Rf_2/(hie・Rb+hie・Rf_2+Rb・Rf_2)
∴Av=vout/vin=(-Rc'・hfe・ib)/((Rin+hie')・ib)=-Rc'・hfe/(Rin+hie')
hieはT=300Kの場合近似的に以下の式で示されます。
hie=kT/q・hfe/Ic=0.03868・hfe/Ic
次に、直流等価回路(下図)よりIcを算出します。
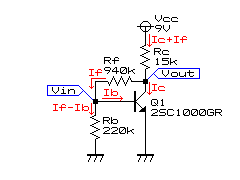
Vbe=(If-Ib)・Rb
⇒ Vbe/Rb=If-Ib
⇒ If=Ib+Vbe/Rb
Vbe=0.6Vとすると、Rb=220kΩより、
∴If=Ib+0.6/220k
Vcc=(Ic+If)・Rc+If・Rf+Vbe
=Ib・hFE・Rc+(Ib+Vbe/Rb)・(Rc+Rf)+Vbe
=Ib・hFE・Rc+Ib・(Rc+Rf)+Vbe・(Rc+Rf)/Rb+Vbe
=Ib・((hFE+1)・Rc+Rf)+Vbe・(Rc+Rf+Rb)/Rb
Vcc-Vbe・(Rc+Rf+Rb)/Rb=Ib・((hFE+1)・Rc+Rf)
⇒ Ib=(Vcc-Vbe・(Rc+Rf+Rb)/Rb)/((hFE+1)・Rc+Rf)
∴Ic=hFE・Ib=hFE・(Vcc-Vbe・(Rc+Rf+Rb)/Rb)/((hFE+1)・Rc+Rf)
Rc=15kΩ,Rf_1=Rf_2=470kΩ,Rf=Rf_1+Rf_2=940kΩ,Rb=220kΩより、
∴Ic=hFE・(Vcc-5.34・Vbe)/(hFE・15k+955k)
hie=0.03868・hfe/Ic=0.03868・hfe/(hFE・(Vcc-5.34・Vbe)/(hFE・15k+955k))
=0.03868・hfe/hFE・(hFE・15k+955k)/(Vcc-5.34・Vbe)
=193.4・hfe/hFE・(hFE・3+191)/(Vcc-5.34・Vbe)
近似的にhfe=hFEと考えると、
hie=193.4・(hFE・3+191)/(Vcc-5.34・Vbe)
2SC1000GRのhFEは200-400なので、今回の計算ではhFE=300と置くことにします。
また、Vcc=9V(006P電池の電圧)、Vbeについては、一般的に0.6-0.7Vぐらいなので、今回の計算ではVbe=0.65Vとします。
hie=193.4・(hFE・3+191)/(Vcc-5.34・Vbe)
=193.4・(300・3+191)/(9-5.34・0.65)
=2.11×105/5.529
=38.2kΩ
hie'=hie・Rb・Rf_2/(hie・Rb+hie・Rf_2+Rb・Rf_2)
=38.2k・220k・470k/(38.2k・220k+38.2k・470k+220k・470k)
=31.0kΩ
Rc'=Rc・Rf_1/(Rc+Rf_1)=15k・470k/(15k+470k)
=14.536k
Av=-Rc'・hfe/(Rin+hie')
=-14.536k・hfe/(15k+31.0k)
=-0.316hfe
∴Av=-94.8
ちなみに、2SC1000GRのhFEを200-400,006P電池の電圧を8.0-9.6V,Vbe=0.6-0.7Vと考えた時には、hieは23.9kΩ(hFE:200,Vcc:9.6V,Vbe:0.6V)から63.1kΩ(hFE:400,Vcc:8V,Vbe:0.7V)、Avは-66.1(hFE:200,Vcc:8.0V,Vbe:0.7V)から-121.5(hFE:400,Vcc:9.6V,Vbe:0.6V)の幅の値をとることになります。さらに、hFEを300に固定して考えた場合でも、依然hie,Avともに33.0kΩ, -103.7(Vcc:9.6V,Vbe:0.6V)から49.5kΩ, -83.5(Vcc:8.0V,Vbe:0.7V)のばらつきが残ります(以上Excelにて計算)。つまり、この程度の概算であまり計算を緻密に行っても現実的な意味は薄いということです。
例えば今回の場合は、以下のようにhie=hie',Rc=Rc'と考えてもさほど結論には影響は出ないことがわかります。
hie=38.2kΩ,hfe=300より、
Av≒-Rc・hfe/(Rin+hie)
=-15k・300/(15k+38.2k)
∴Av=-84.6
以上の計算結果を踏まえて、Avについての計算式を簡単に解析してみます。
Av=-Rc'・hfe/(Rin+hie')≒-Rc・hfe/(Rin+hie)
入力電圧vinは、RinとQ1の入力インピーダンスhieで分圧されてhie/(Rin+hie)倍になってQ1に入力されます。Q1に入力された電圧vb=hie/(Rin+hie)・vinは、入力インピーダンスhieにより入力電流ib=vb/hie=hie/(Rin+hie)・vin/hie=1/(Rin+hie)・vinに変換されます。トランジスタQ1は入力電流ibのhfe倍をコレクタに流す作用があるので、コレクタに流れる電流は、ic=hfe・ib=hfe/(Rin+hie)・vinとなります。このコレクタ電流icは、Rcにて出力電圧vout=-Rc・hfe/(Rin+hie)・vinに変換されます(電圧変位の基準がVccになるので、位相が反転する)。
ゆえに電圧増幅率Avは、近似的にAv=vout/vin≒-Rc・hfe/(Rin+hie)で求められることになるわけです。
ちなみに10μF電解コンデンサがない時の増幅率は、交流等価回路(下図)より以下のように算出できます。
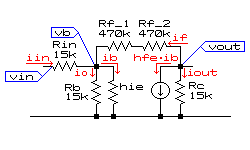
vin=iin・Rin+vb=(ib+if-i0)・Rin+vb
vb=ib・hie=i0・Rb
⇒ i0=hie/Rb・ib
∴vin=(ib+if-i0)・Rin+vb=(ib・hie/Rb+ib+if)・Rin+ib・hie
=(Rin+hie+Rin/Rb・hie)・ib+Rin・if
vout=-if・Rf+vb=-if・Rf+ib・hie
vout=-iout・Rc=(-hfe・ib+if)・Rc
⇒ (-hfe・ib+if)・Rc=-if・Rf+ib・hie
⇒ (hfe・Rc+hie)・ib=if・(Rc+Rf)
hfe・Rc≫hieなので、hfe・Rc+hieの部分のhieを無視すると、ifとibの関係式が以下のように求められます。
∴if=hfe・Rc/(Rc+Rf)・ib
このifとibの関係式を使って、vinおよびvoutの式のifを消去します。
vin=(Rin+hie+Rin/Rb・hie)・ib+Rin・hfe・Rc/(Rc+Rf)・ib
=((Rin+hie+Rin/Rb・hie)+Rin・hfe・Rc/(Rc+Rf))・ib
vout=-if・Rf+ib・hie=-hfe・Rc・Rf/(Rc+Rf)・ib+hie・ib
=-hfe・Rc・Rf/(Rc+Rf)・ib+hie・ib
=(hie-hfe・Rc・Rf/(Rc+Rf))・ib
Av'=vout/vin=(hie-hfe・Rf・Rc/(Rc+Rf)・ib)/(((Rin+hie+Rin/Rb・hie)-Rin・hfe・Rc/(Rc+Rf))・ib)
=(hie-hfe・Rf・Rc/(Rc+Rf))/((Rin+hie+Rin/Rb・hie)+Rin・hfe・Rc/(Rc+Rf))
=(hie・(Rc+Rf)-hfe・Rf・Rc)/((Rin+hie+Rin/Rb・hie)・(Rc+Rf)+Rin・hfe・Rc)
10μF電解コンデンサがあろうとなかろうと直流等価回路に違いはないので、hieは上の10μF電解コンデンサがある場合の結果と同じになります。よって、hFE=300の場合、33.0kΩ≦hie≦49.5kΩになります。
ここでは、上と同様にhFE=300,Vcc=9V,Vbe=0.65Vの時のhie=38.2kΩ を使用して以下の計算を行うこととします。
Rin=15kΩ,Rb=220kΩ,Rf=940kΩ,Rc=15kΩ,hfe=300より、
Av'=(hie・(Rc+Rf)-hfe・Rf・Rc)/((Rin+hie+Rin/Rb・hie)・(Rc+Rf)+Rin・hfe・Rc)
=(38.2k・(15k+940k)-hfe・940k・15k)/((15k+38.2k+15k/220k・38.2k)・(15k+940k)+15k・hfe・15k)
=(36481-15100・hfe)/(53254+225・hfe)
∴Av'=-37.2
上と同様にAv'についての計算式を簡略化してみます。
Av'=(hie・(Rc+Rf)-hfe・Rf・Rc)/((Rin+hie+Rin/Rb・hie)・(Rc+Rf)+Rin・hfe・Rc)
hfe・Rf・Rc≫hie・(Rc+Rf)なので、hie・(Rc+Rf)を無視すると、
Av'≒-hfe・Rf・Rc/((Rin+hie+Rin/Rb・hie)・(Rc+Rf)+Rin・hfe・Rc)
=-hfe・Rf・Rc/((Rin+hie+Rin/Rb・hie)・(Rc+Rf)+Rin・hfe・Rc)
Rin/Rb≪1,Rc≪Rfより、
Av'≒-hfe・Rf・Rc/((Rin+hie)・Rf+Rin・hfe・Rc)
=-hfe・Rf・Rc/(Rin・Rf+hie・Rf+Rin・hfe・Rc)
=-hfe・Rf・Rc/(Rin・(Rf+hfe・Rc)+hie・Rf)
=-hfe・Rf・Rc/(Rin・hfe・Rc+(Rin+hie)・Rf)
=-Rf/(Rin+(Rin+hie)・Rf/(hfe・Rc))
∴Av'≒-Rf/(Rin+(Rin+hie)・Rf/(hfe・Rc))
この簡略化された式でAv'を算出すると、以下のようになります。(意外といい線行っていると思うのですが、いかがでしょう??)
Av'≒-940k/(15k+(15k+38.2k)・940k/(300・15k))=-36.0
以上の計算結果を踏まえて、Av'についての計算式を解析してみます。
まず、この回路を負帰還増幅回路と捉えてみます。負帰還増幅回路の増幅率Gは以下の式で求められます(参考文献1:pp52-57より)。
A:オープンループゲイン,β:帰還率,Gideal:理想オペアンプを使用した時のクローズドループゲイン とすると、
G=Gideal・(1/(1+1/Aβ))
反転増幅回路の場合、Gideal=1-1/β なので、
G=Gideal・(1/(1+1/Aβ))
=(1-1/β)・(1/(1+1/Aβ))
=(β-1)/β・1/(1+1/Aβ)
=(β-1)/(β+1/A)
=A・(β-1)/(Aβ+1)
オープンループゲインAは、Rfを取っ払って無帰還にした時のこの回路の増幅率に等しいと考えられます。帰還経路にあまり関係しないRbを無視すると、
vb=hie・ib
vin=(Rin+hie)/hie・vb
=(Rin+hie)/hie・hie・ib
=(Rin+hie)・ib
vout=-Rc・hfe・ib
A=|vout/vin|=|-Rc・hfe・ib/((Rin+hie)・ib)|
=Rc・hfe/(Rin+hie)
帰還率βは、帰還抵抗をRf、入力抵抗をRinとして簡単に考えることにより、以下のようになります。
β=Rin/(Rin+Rf)
G=(β-1)/(β+1/A)
=(Rin/(Rin+Rf)-1)/(Rin/(Rin+Rf)+1/(Rc・hfe/(Rin+hie)))
=(-Rf/(Rin+Rf))/(Rin/(Rin+Rf)+(Rin+hie)/(Rc・hfe))
=-Rf/(Rin+(Rin+Rf)・(Rin+hie)/(Rc・hfe))
=-Rf/(Rin+(Rin+hie)・(Rin+Rf)/(hfe・Rc))
Rin≪Rfなので、
∴G=-Rf/(Rin+(Rin+hie)・Rf/(hfe・Rc))
これは、上で求めたAv'の式と同じになります。
ゆえに、オープンループゲインA=無帰還時の増幅率、帰還率β=Rin/(Rin+Rf) および Gideal=1-1/β として負帰還増幅回路を考えることにより、電圧増幅率Av'が近似的に求められることになります。
<2段目トランジスタ回路の増幅率および入力インピーダンスについて>
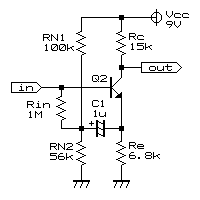
上の回路を交流等価回路(下図)に書き直します。
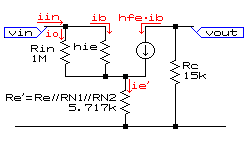
ReとRN1とRN2の並列合成抵抗をRe'とすると、
Re'=Re‖RN1‖RN2
=1/(1/Re+1/RN1+1/RN2)
vin=ib・hie+(i0+ib+hfe・ib)・Re'
i0・Rin=ib・hie
⇒ i0=hie/Rin・ib
∴vin=ib・hie+(i0+ib+hfe・ib)・Re'
=ib・hie+(hie/Rin・ib+ib+hfe・ib)・Re'
=ib・(hie+(hie/Rin+1+hfe)・Re')
=ib・(hie・(Rin+Re')+(hfe+1)・Re'・Rin)/Rin
vout=-Rc・hfe・ib
この回路の電圧増幅率Avは、
Av=vout/vin=-Rc・hfe・ib/(ib・(hie・(Rin+Re')+(hfe+1)・Re'・Rin)/Rin)
=-Rc・hfe・Rin/(hie・(Rin+Re')+(hfe+1)・Re'・Rin)
Rin≫Re',hfe≫1なので、Rin+Re'≒Rin,hfe+1≒hfeとすると、
Av≒-Rc・hfe・Rin/(hie・Rin+hfe・Re'・Rin)
=-Rc/(hie/hfe+Re')
∴Av≒-Rc/(hie/hfe+Re')
ちなみにhieはだいたい数十kΩ、hfeは200-400なので、hie/hfeはせいぜい数百程度ですが、Re'は5.717kΩなのでRe'≫hie/hfeになります。よってhie/hfeを無視すると、概算のAvを求めることができます。
(hie/hfeを無視した場合、Av≒-Rc/Re'=-15k/5.717k=-2.6)
次に、入力インピーダンスZinを求めます。
vin=ib・(hie・(Rin+Re')+(hfe+1)・Re'・Rin)/Rin
i0=hie/Rin・ib
⇒ iin=ib+i0=ib+hie/Rin・ib
=(Rin+hie)/Rin・ib
Zin=vin/iin=(ib・(hie・(Rin+Re')+(hfe+1)・Re'・Rin)/Rin)/((Rin+hie)/Rin・ib)
=(hie・(Rin+Re')+(hfe+1)・Re'・Rin)/(Rin+hie)
Rin≫Re',hfe≫1なので、Rin+Re'≒Rin,hfe+1≒hfeとすると、
∴Zin=(hie・Rin+hfe・Re'・Rin)/(Rin+hie)
=(hie+hfe・Re')・Rin/(Rin+hie)
このとき、hieはだいたい数十kΩなのでRin≫hie、hfeは200-400なのでhfe・Re'≫hieとなる。よってhieを無視すると、概略の入力インピーダンスZinが算出できます。
(hfe=300のとき、Zin≒hfe・Re'=1.7M)
直流等価回路(下図)よりIcを算出します。
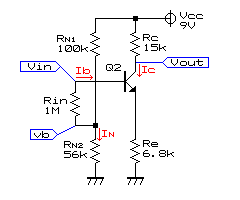
Vcc=(IN+Ib)・RN1+IN・RN2
=IN・(RN1+RN2)+Ib・RN1
IN=(Vcc-Ib・RN1)/(RN1+RN2)
Vb=IN・RN2=Vin-Ib・Rin
Vin=IN・RN2-Ib・Rin
=RN2・(Vcc-Ib・RN1)/(RN1+RN2)-Ib・Rin
=RN2/(RN1+RN2)・Vcc-(RN1・RN2/(RN1+RN2)+Rin)・Ib
Vin=Vbe+(hFE+1)・Ib・Re
Vbe+(hFE+1)・Ib・Re=RN2/(RN1+RN2)・Vcc-(RN1・RN2/(RN1+RN2)+Rin)・Ib
RN2/(RN1+RN2)・Vcc-Vbe=(hFE+1)・Ib・Re+(RN1・RN2/(RN1+RN2)+Rin)・Ib
=((hFE+1)・Re+Rin+(RN1・RN2/(RN1+RN2))・Ib
∴Ib=(RN2/(RN1+RN2)・Vcc-Vbe)/((hFE+1)・Re+Rin+(RN1・RN2/(RN1+RN2))
ここで、Rin≫RN1‖RN2=(RN1・RN2/(RN1+RN2),hFE≫1と考えると、分母≒Rin+hFE・Reとすることができる。よって、
∴Ib=(RN2/(RN1+RN2)・Vcc-Vbe)/(Rin+hFE・Re)
Rin=1MΩ,RN1=100kΩ,RN2=56kΩ,Re=6.8kΩ,Rc=15kΩより、Vcc=9V,Vbe=0.65Vとして値を代入すると、
Ib=(RN2/(RN1+RN2)・Vcc-Vbe)/(Rin+hFE・Re)
=(56k/(100k+56k)・9-0.65)/(1M+6.8k・hFE)
=2.58/(1M+6.8k・hFE)
(hFEを300とすると、Ib=2.58/(1M+6.8k・300)=0.848μA)
Ic=hFE・Ib=2.58・hFE/(1M+6.8k・hFE)
(hFEを300とすると、Ic=2.58・hFE/(1M+6.8k・hFE)=0.2546mA)
hie=0.03868・hfe/Ic=0.03868・hfe/(hFE・Ib)
=0.03868/Ib
=0.03868/(2.58/(1M+6.8k・hFE))
=0.03868・(1M+6.8k・hFE)/2.58
=0.015・(1M+6.8k・hFE)
=15k+102・hFE
(hFEを300とすると、hie=15k+102・300=45.6kΩ)
以上の結果より、hFE=300の時の電圧増幅率Av および 入力インピーダンスZinを算出します。
Av≒-Rc/(hie/hfe+Re')
=-15k/(45.6k/300+5.717k)
=-2.556
Zin=(hie+hfe・Re')・Rin/(Rin+hie)
=(45.6K+300・5.717k)・1M/(45.6k+1M)
=1.68M
このように入力インピーダンスが高くなっている理由は、C1により入力に対してブートストラップ(正帰還)をかけることでRinの両端に同相の信号が加わり、Rinに電流が流れなくなるためRinがつながっていないのと同じような状態になることによります。
エフェクタにおける初段の回路のように、前段になにがつながれるかわからない状態でこのような回路を使うのは、(ブートストラップが正帰還であるがゆえに)発振の危険をいたずらに増やすことになりそうですが、2段目以降のように前段の回路が固定ならば、それなりに有効な気がします。ただ、この部分がそんなに高いインピーダンスを求められているようにも思えないのですが。
C1がつながっていない状態(ブートストラップがかかっていない状態)での回路解析も同様に行って、結果を比較してみます。
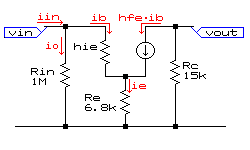
上の交流等価回路より、
vin=ib・hie+(hfe+1)・ib・Re
=ib・(hie+(hfe+1)・Re)
vout=-Rc・hfe・ib
Av'=vout/vin=-Rc・hfe・ib/ib・(hie+(hfe+1)・Re)
=-Rc・hfe/(hie+(hfe+1)・Re)
hfe≫1なので、hfe+1≒hfeとすると、
Av'≒-Rc・hfe/(hie+hfe・Re)
=-Rc/(hie/hfe+Re)
∴Av'≒-Rc/(hie/hfe+Re)
ブートストラップありの場合の電圧増幅率がAv≒-Rc/(hie/hfe+Re')であったことを考えると、電圧増幅率については、ブートストラップあり/なしによる相違は少ない(概ねReとRe'の違いの分だけ異なる)ことがわかります。
ちなみにブートストラップありの時の計算と同様、hieはだいたい数十kΩ、hfeは200-400なので、hie/hfeはせいぜい数百程度ですが、Reは6.8kΩなのでRe≫hie/hfeになります。よってhie/hfeを無視すると、概算のAv'を求めることができます。
(hie/hfeを無視した場合、Av'≒-Rc/Re=-15k/6.8k=-2.2)
次に、入力インピーダンスZin'を求めます。
vin=ib・(hie+(hfe+1)・Re)
vin=i0・Rin
i0・Rin=ib・(hie+(hfe+1)・Re)
⇒ i0=ib・(hie+(hfe+1)・Re)/Rin
iin=i0+ib
=ib・(hie+(hfe+1)・Re)/Rin+ib
=ib・(Rin+hie+(hfe+1)・Re)/Rin
Zin'=vin/iin=ib・(hie+(hfe+1)・Re)/(ib・(Rin+hie+(hfe+1)・Re)/Rin)
=Rin・(hie+(hfe+1)・Re)/(Rin+hie+(hfe+1)・Re)
hfe≫1なので、hfe+1≒hfeとすると、
∴Zin'=Rin・(hie+hfe・Re)/(Rin+(hie+hfe・Re))
=Rin‖(hie+hfe・Re)
上記より、Zin'はRinと(hie+hfe・Re)の並列合成抵抗にほぼ等しいことがわかります。
ブートストラップありの回路もなしの回路も直流等価回路は同じなので、hieの計算結果をそのまま利用できます。hfe=300の時hie=45.6kΩなので、
hie/hfe=45.6k/300
=152
∴Av'≒-Rc/(hie/hfe+Re)
=-15k/(152+6.8k)=2.16
hie+hfe・Re=45.6k+300・6.8k
=2.04M+45.6k
=2.09M
∴Zin'=Rin・(hie+hfe・Re)/(Rin+(hie+hfe・Re))
=(2.09M・1M)/(2.09M+1M)=676k
以上の結果を踏まえて、ブートストラップあり回路の結果とブートストラップなし回路の入力インピーダンスを比較してみます。
<ブートストラップあり>
Zin=(hie+hfe・Re')・Rin/(Rin+hie)
<ブートストラップなし>
Zin'=(hie+hfe・Re)・Rin/(Rin+(hie+hfe・Re))
=(hie+hfe・Re)・Rin/(Rin+hie)・(Rin+hie)/(Rin+(hie+hfe・Re))
Re≒Re'と考えて、ReをRe'で置きかえると、
Zin'=(hie+hfe・Re')・Rin/(Rin+hie)・(Rin+hie)/(Rin+(hie+hfe・Re))
=Zin・(Rin+hie)/(Rin+Zin・(Rin+hie)/Rin)
=1/(Rin/(Zin・(Rin+hie))+1/Rin)
Rin≫hieと考えて、Rin+hie=Rinと置くと、
Zin'=1/(Rin/(Zin・(Rin+hie))+1/Rin)
=1/(Rin/Zin・Rin+1/Rin)
=1/(1/Zin+1/Rin)
∴Zin'≒Zin‖Rin
以上の結果より、ブートストラップなしの回路はブートストラップありの回路に比べて、概ねRinが並列にかかる分だけ入力インピーダンスが低下していることがわかります。
(上で無視した交流等価回路におけるエミッタ抵抗の相対的な低下(ReとRe'の差)も多少影響しますが)
参考文献1:トランジスタ技術SPECIAL増刊:OPアンプによる実用回路設計(馬場 清太郎著、CQ出版社)
Roland BeeGee
<Slightly MOD Versionの説明>
さすがに今の時代、ゲイン最大固定はキツイような気がします。
まあ潔いとも言えなくはないですが。
あとOUTを絞ったときに音量がゼロにならないのも気持ち悪いといえば
気持ち悪いように思います。
というわけで、わたしは上の回路図にあるようなMODをしてみました。
オペアンプの帰還抵抗を可変にして、かつOUTの47Ωを取っ払いました。
可変抵抗に直列に接続されている固定抵抗は、ゲインの可変範囲(minimum)を
決定します。47k-200kΩの間で好みに応じて設定してください。
オリジナルを尊重するならば、実機の抵抗値が2.2MΩなので可変2MΩ+固定200kΩ
としたいところですが、ゲインの低い時の音も結構使えるように感じられたので、
わたし自身は47kΩに設定しました。
Supatonebender1978
いわゆるBigMuff型の回路です。トランジスタ1石増幅回路×3でしこたまゲインを稼いだ後、ハイパス+ローパスフィルタで構成されるトーン回路を経て、終段のバッファ(?)で多少ゲインを稼ぐ感じになっています。
本家BigMuffとの回路上の違いは、BigMuffのクリップダイオードは2段目と3段目についていますが、SupaTonebenderにおいては3段目(上図Q3)しかついていないところにあります。あと細かな定数が多少違います。多少の違い、と言っても、クリップダイオードに直接ついているコンデンサ(この回路におけるC8)やトーンまわりの定数相違は、音色に直接効いてきます。
1〜3段目の増幅回路については、下記<1〜3段目の増幅回路の解析>を参照してください。
トーン回路は、(上図C10,R18により構成される)パッシブハイパスフィルタと(上図R17,C11により構成される)パッシブのローパスフィルタの出力を可変抵抗(上図VR2)でブレンドする形になっています。見た目単純ですが、うまく定数を設定するとトーンのツマミの位置によってはフラットな出力を得る事ができるようになります。フィルタの伝達関数については、みなさん是非一度は計算してみて欲しいところです。
最終段はよくトランジスタの本で見かける電流帰還バイアス回路です。おおむね増幅率はR21/R22,入力インピーダンスはhieに,出力インピーダンスはR21程度になります。パッシブフィルタにより結果的に下がった出力信号と上がった出力インピーダンスを多少リカバーしているようです。特に出力インピーダンスについては、これで十分とは言えないような気もしますが、まあ無いよりはマシか、という感じでしょう。
<1〜3段目の増幅回路の解析>
1〜3段目の増幅回路において、交流等価回路は下図のようになります。
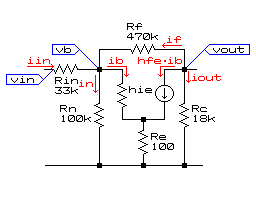
vb=in・Rn=ib・(hie+(hfe+1)・Re)
Rx=hie+(hfe+1)・Reと置くと
vb=in・Rn=ib・Rx
⇒ in=ib・Rx/Rn
iin=in+ib-if
vout=-(hfe・ib-if)・Rc
vb=vout-if・Rf
=-(hfe・ib-if)・Rc-if・Rf
=-hfe・ib・Rc+if・(Rc-Rf)
=-hfe・ib・Rc-if・(Rf-Rc)
-hfe・ib・Rc-if・(Rf-Rc)=ib・Rx
-if・(Rf-Rc)=ib・(Rx+hfe・Rc)
if=-ib・(Rx+hfe・Rc)/(Rf-Rc)
vout=-(hfe・ib-if)・Rc
=-{hfe・ib+ib・(Rx+hfe・Rc)/(Rf-Rc)}・Rc
=-ib・{hfe・(Rf-Rc)+(Rx+hfe・Rc)}・Rc/(Rf-Rc)
=-ib・(hfe・Rf+Rx)・Rc/(Rf-Rc)
iin=in+ib-if
=ib・Rx/Rn+ib+ib・(Rx+hfe・Rc)/(Rf-Rc)
=ib・(Rx+Rn)・(Rf-Rc)/{Rn・(Rf-Rc)}+ib・Rn・(Rx+hfe・Rc)/{Rn・(Rf-Rc)}
=ib・{(Rx+Rn)・(Rf-Rc)+Rn・(Rx+hfe・Rc)}/{Rn・(Rf-Rc)}
vin=iin・Rin+vb
=ib・{(Rx+Rn)・(Rf-Rc)+Rn・(Rx+hfe・Rc)}/{Rn・(Rf-Rc)}・Rin+ib・Rx
=ib・{(Rx+Rn)・(Rf-Rc)+Rn・(Rx+hfe・Rc)}/{Rn・(Rf-Rc)}・Rin+ib・Rx・Rn・(Rf-Rc)/{Rn・(Rf-Rc)}
=ib・[{(Rx+Rn)・(Rf-Rc)+Rn・(Rx+hfe・Rc)}・Rin+Rx・Rn・(Rf-Rc)]/{Rn・(Rf-Rc)}
=ib・[(Rx+Rn)・(Rf-Rc)・Rin+Rn・(Rx+hfe・Rc)・Rin+Rx・Rn・(Rf-Rc)]/{Rn・(Rf-Rc)}
=ib・[{(Rx+Rn)・Rin+Rx・Rn}・(Rf-Rc)+Rn・Rin・(Rx+hfe・Rc)]/{Rn・(Rf-Rc)}
=ib・{(Rx・Rin+Rn・Rin+Rx・Rn)・(Rf-Rc)+Rn・Rin・(Rx+hfe・Rc)}/{Rn・(Rf-Rc)}
Av=vout/vin=-(hfe・Rf+Rx)・Rc/(Rf-Rc)・ib/[ib・{(Rx・Rin+Rn・Rin+Rx・Rn)・(Rf-Rc)+Rn・Rin・(Rx+hfe・Rc)}/{Rn・(Rf-Rc)}]
=-(hfe・Rf+Rx)・Rc・Rn/{(Rx・Rin+Rn・Rin+Rx・Rn)・(Rf-Rc)+Rn・Rin・(Rx+hfe・Rc)}
=-(hfe・Rf+Rx)・Rc/{(Rx・Rin+Rx・Rn+Rin・Rn)・(Rf-Rc)/Rn+Rin・(Rx+hfe・Rc)}
Rf≫Rc,hfe・Rf≫Rx,hfe・Rc≫Rxより、Rf-Rc=Rf,hfe・Rf+Rx=hfe・Rx,Rx+hfe・Rc=hfe・Rcと置くと、
Av=-(hfe・Rf+Rx)・Rc/{(Rx・Rin+Rx・Rn+Rin・Rn)・(Rf-Rc)/Rn+Rin・(Rx+hfe・Rc)}
≒-hfe・Rf・Rc/{(Rx・Rin+Rx・Rn+Rin・Rn)・Rf/Rn+hfe・Rc・Rin}
=-1/{(Rx・Rin+Rx・Rn+Rin・Rn)/(Rn・Rc・hfe)+Rin/Rf}
以上の計算結果を踏まえて、Avについての計算式を解析してみます。
まず、この回路を負帰還増幅回路と捉えてみます。負帰還増幅回路の増幅率Gは以下の式で求められます(参考文献1:pp52-57より)。
A:オープンループゲイン,β:帰還率,Gideal:理想オペアンプを使用した時のクローズドループゲイン とすると、
G=Gideal・(1/(1+1/Aβ))
反転増幅回路の場合、Gideal=1-1/β なので、
G=Gideal・(1/(1+1/Aβ))
=(1-1/β)・(1/(1+1/Aβ))
=(β-1)/β・1/(1+1/Aβ)
=(β-1)/(β+1/A)
=A・(β-1)/(Aβ+1)
オープンループゲインAは、Rfを取っ払って無帰還にした時のこの回路の増幅率に等しいと考えられます。よって、
vb=hie・ib+(hfe+1)・ib・Re
=(hie+(hfe+1)・Re)・ib
=Rx・ib
Rn‖Rx=Rn・Rx/(Rn+Rx)
vin=(Rin+Rn‖Rx)/(Rn‖Rx)・vb
=(Rin+Rn・Rx/(Rn+Rx))/(Rn・Rx/(Rn+Rx))・vb
=(Rin+Rn・Rx/(Rn+Rx))/(Rn・Rx/(Rn+Rx))・Rx・ib
=(Rin・(Rn+Rx)+Rn・Rx)/(Rn・Rx)・Rx・ib
=(Rin・(Rn+Rx)+Rn・Rx)/Rn・ib
=(Rx・Rin+Rx・Rn+Rin・Rn)/Rn・ib
vout=-Rc・hfe・ib
A=|vout/vin|=|-Rc・hfe・ib/((Rx・Rin+Rx・Rn+Rin・Rn)/Rn・ib)|
=hfe・Rc・Rn/(Rx・Rin+Rx・Rn+Rin・Rn)
帰還率βは、帰還抵抗をRf、入力抵抗をRinとして簡単に考えることにより、以下のようになります。
β=Rin/(Rin+Rf)
G=(β-1)/(β+1/A)
={Rin/(Rin+Rf)-1}/[Rin/(Rin+Rf)+1/{hfe・Rc・Rn/(Rx・Rin+Rx・Rn+Rin・Rn)}]
={-Rf/(Rin+Rf)}/[Rin/(Rin+Rf)+1/{hfe・Rc・Rn/(Rx・Rin+Rx・Rn+Rin・Rn)}]
=-Rf/{Rin+(Rx・Rin+Rx・Rn+Rin・Rn)・(Rin+Rf)/(hfe・Rc・Rn)}
=-hfe・Rc・Rf/{(Rx・Rin+Rx・Rn+Rin・Rn)・(Rin+Rf)/Rn+hfe・Rc・Rin}
=-hfe・Rf・Rc/((Rx・Rin+Rx・Rn+Rin・Rn)・(Rin+Rf)/Rn+hfe・Rc・Rin)
Rin≪Rfなので、
∴G=-hfe・Rf・Rc/((Rx・Rin+Rx・Rn+Rin・Rn)・Rf/Rn+hfe・Rc・Rin)
これは、上で求めたAvの式と同じになります。
ゆえに、オープンループゲインA=無帰還時の増幅率、帰還率β=Rin/(Rin+Rf) およびGideal=1-1/β として負帰還増幅回路を考えることにより、電圧増幅率Avが近似的に求められることになります。
次に回路の入力インピーダンスZ(Zin)を求めます。
Zin=vin/iin=Rin+vb/iin
=Rin+ib・Rx/[ib・{(Rx+Rn)・(Rf-Rc)+Rn・(Rx+hfe・Rc)}/{Rn・(Rf-Rc)}]
=Rin+Rx・Rn・(Rf-Rc)/{(Rx+Rn)・(Rf-Rc)+Rn・(Rx+hfe・Rc)}
以下、Zinをざっくり求めてみます。
Rf≫Rc,hfe・Rc≫Rxより、Rf-Rc=Rf, Rx+hfe・Rc=hfe・Rcと置くと、
Zin=Rin+Rx・Rn・(Rf-Rc)/{(Rx+Rn)・(Rf-Rc)+Rn・(Rx+hfe・Rc)}
≒Rin+Rx・Rn・Rf/{(Rx+Rn)・Rf+Rn・hfe・Rc}
hfe・Rc≫Rfより、分母のhfe・Rc以外の項を無視すると、
Zin≒Rin+Rx・Rn・Rf/{(Rx+Rn)・Rf+Rn・hfe・Rc}
=Rin+Rx・Rn・Rf/(Rn・hfe・Rc)
=Rin+Rx・Rf/(hfe・Rc)
∴Zin≒Rin+Rx・Rf/(hfe・Rc)
hfeは数百のオーダー、かつRxは数十kΩのオーダーなので、Rx・Rf/(hfe・Rc)の項は概ね数kΩのオーダーになります。
よって回路の入力Z(Zin)をざっくりと計算すると、1段目の増幅回路においてはRinが33kΩなので、入力ZはほぼRinによって決定されます。また、2〜3段目の増幅回路では、Rinが8.2kΩなので、入力ZはせいぜいRin〜Rin×2ぐらいと予測できます。
しかし、エフェクタ自体の入力Zが33kΩ+αというのは、ギターの出力(パッシブの場合、大抵数百kΩ程度)を直接受けるにはかなり低いと思います。インピーダンスのアンマッチによるハイ落ちもこの形の歪みモノの音色に寄与しているようです。
hie=0.03868・hFE/Icよりhieを算出するため、下の直流等価回路よりIcを求めることにします。
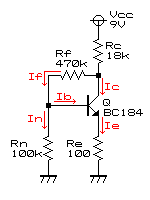
(If-Ib)・Rn=Vbe+Ie・Re=Vbe+(hFE+1)・Ib・Re
If-Ib=Vbe/Rn+(hFE+1)・Ib・Re/Rn
If=Vbe/Rn+((hFE+1)・Re/Rn+1)・Ib
Vcc=Rc・(Ic+If)+If・Rf+In・Rn
=Rc・(hFE・Ib+If)+If・Rf+(If-Ib)・Rn
=(Rc・hFE-Rn)・Ib+(Rc+Rf+Rn)・If
=(Rc・hFE-Rn)・Ib+(Rc+Rf+Rn)・[Vbe/Rn+{(hFE+1)・Re/Rn+1}・Ib]
=(Rc+Rf+Rn)/Rn・Vbe+[Rc・hFE-Rn+(Rc+Rf+Rn)・{(hFE+1)・Re/Rn+1}]・Ib
=(Rc+Rf+Rn)/Rn・Vbe+{Rc・hFE-Rn+Rc+Rf+Rn+(Rc+Rf+Rn)・(hFE+1)・Re/Rn}・Ib
=(Rc+Rf+Rn)/Rn・Vbe+{(hFE+1)・Rc+Rf+(Rc+Rf+Rn)・(hFE+1)・Re/Rn}・Ib
hFE≫1より、hFE+1=hFEと置くと、
Vcc=(Rc+Rf+Rn)/Rn・Vbe+{(hFE+1)・Rc+Rf+(Rc+Rf+Rn)・(hFE+1)・Re/Rn}・Ib
=(Rc+Rf+Rn)/Rn・Vbe+{hFE・Rc+Rf+(Rc+Rf+Rn)/Rn・hFE・Re}・Ib
Vcc-(Rc+Rf+Rn)/Rn・Vbe={hFE・Rc+Rf+(Rc+Rf+Rn)/Rn・hFE・Re}・Ib
Ib={Vcc-(Rc+Rf+Rn)/Rn・Vbe}/{hFE・Rc+Rf+(Rc+Rf+Rn)/Rn・hFE・Re}
∴Ic=hFE・Ib=hFE・{Vcc-(Rc+Rf+Rn)/Rn・Vbe}/{hFE・Rc+Rf+(Rc+Rf+Rn)/Rn・hFE・Re}
={Vcc-(Rc+Rf+Rn)/Rn・Vbe}/{Rc+Rf/hFE+(Rc+Rf+Rn)/Rn・Re}
Rf≫Rcより、Rc+Rf=Rfと置くと、
Ic={Vcc-(Rc+Rf+Rn)/Rn・Vbe}/{Rc+Rf/hFE+(Rc+Rf+Rn)/Rn・Re}
={Vcc-(Rf+Rn)/Rn・Vbe}/{Rc+Rf/hFE+(Rf+Rn)/Rn・Re}
Rc≫(Rc+Rf+Rn)/Rn・Reより、Reを無視すると、
Ic={Vcc-(Rf+Rn)/Rn・Vbe}/{Rc+Rf/hFE+(Rf+Rn)/Rn・Re}
={Vcc-(Rf+Rn)/Rn・Vbe}/(Rc+Rf/hFE)
hie=0.03868・hFE/Ic
=0.03868・hFE/[{Vcc-(Rf+Rn)/Rn・Vbe}/(Rc+Rf/hFE)]
=0.03868・hFE・(Rc+Rf/hFE)/{Vcc-(Rf+Rn)/Rn・Vbe}
=(0.03868・hFE・Rc+0.03868・Rf)/{Vcc-(Rf+Rn)/Rn・Vbe}
Vcc=9V,Vbe=0.65Vとすると、Rf=470kΩ,Rn=100kΩより、
hie=(0.03868・hFE・Rc+0.03868・Rf)/{Vcc-(Rf+Rn)/Rn・Vbe}
=(0.03868・hFE・Rc+0.03868・470k)/{9-(470k+100k)/100k・0.65}
=(0.03868・hFE・Rc+0.03868・470k)/5.295
=0.007305・hFE・Rc+3433
hfe≫1なのでhfe+1=hfeとすると、
Rx=hie+(hfe+1)・Re≒hie+hfe・Re
=0.007305・hFE・Rc+3433+hfe・Re
=hFE・(0.007305・Rc+Re)+3433
1段目の増幅回路においては、Rin=33kΩ,Rn=100kΩ,Rf=470kΩ,Rc=18kΩ,Re=100Ωなので、
Rx=hFE・(0.007305・Rc+Re)+3433
=hFE・(0.007305・18k+100)+3433
=231・hFE+3433
Av1=-1/{(Rx・Rin+Rx・Rn+Rin・Rn)/(Rn・Rc・hfe)+Rin/Rf}
=-1/[{(231・hFE+3433)・133k+33k・100k}/(100k・18k・hfe)+33k/470k]
=-1/{(231・hFE・133k+3433・133k+33k・100k)/(100k・18k・hfe)+0.0702}
=-1/{(30.723・hFE+3756)/(1800・hfe)+0.0702}
=-1/(0.0170+2.087/hfe+0.0702)
=-1/(0.0872+2.087/hfe)
∴Av1=-1/(0.0872+2.087/hfe)
=-10.6 (hFE=300のとき)
∴Zin1=Rin+Rx・Rn・(Rf-Rc)/{(Rx+Rn)・(Rf-Rc)+Rn・(Rx+hfe・Rc)}
=33k+(231・hFE+3433)・100k・(470k-18k)/{(231・hFE+3433+100k)・(470k-18k)+100k・(231・hFE+3433+hfe・18k)}
=33k+(231・hFE+3433)・100k・452k/{(231・hFE+103.4k)・452k+100k・(18231・hFE+3433)}
=33k+(231・hFE+3433)・100k・452k/(231・452k・hFE+100k・18231・hFE+103.4k・452k+100k・3433)
=33k+(231・hFE+3433)・45200M/(1927.5M・hFE+47080.1M)
=33k+(10441k・hFE+155171k)/(1927.5・hFE+47080.1)
=38.2k (hFE=300のとき)
同様に2段目,3段目の増幅回路についてAvおよびZinを算出します。2段目はRin=8.2kΩ,Rn=100kΩ,Rf=470kΩ,Rc=10kΩ,Re=100Ωなので、
Rx=hFE・(0.007305・Rc+Re)+3433
=173・hFE+3433
∴Av2=-1/{(Rx・Rin+Rx・Rn+Rin・Rn)/(Rn・Rc・hfe)+Rin/Rf}
=-1/[{(173・hFE+3433)・108.2k+8.2k・100k}/(100k・10k・hfe)+8.2k/470k]
=-1/[0.0187+1.1914/hfe+0.0174]
=-1/(0.0361+1.1914/hfe)
=-24.9 (hFE=300のとき)
∴Zin2=Rin+Rx・Rn・(Rf-Rc)/{(Rx+Rn)・(Rf-Rc)+Rn・(Rx+hfe・Rc)}
=8.2k+(173・hFE+3433)・100k・(470k-10k)/{(173・hFE+3433+100k)・(470k-10k)+100k・(173・hFE+3433+hfe・10k)}
=8.2k+(79580・hFE+1579k)/(10.9688・hFE+479)
=14.9k (hFE=300のとき)
3段目はRin=8.2kΩ,Rn=100kΩ,Rf=470kΩ,Rc=18kΩ,Re=100Ωなので、
Rx=hFE・(0.007305・Rc+Re)+3433
=hFE・(0.007305・18k+100)+3433
=231・hFE+3433
∴Av3=-1/{(Rx・Rin+Rx・Rn+Rin・Rn)/(Rn・Rc・hfe)+Rin/Rf}
=-1/[{(231・hFE+3433)・133k+33k・100k}/(100k・18k・hfe)+8.2k/470k]
=-1/{(0.0139+0.6619/hfe+0.0174}
=-1/(0.0313+0.6619/hfe)
=-29.8 (hFE=300のとき)
∴Zin3=Rin+Rx・Rn・(Rf-Rc)/{(Rx+Rn)・(Rf-Rc)+Rn・(Rx+hfe・Rc)}
=8.2k+(231・hFE+3433)・100k・(470k-18k)/{(231・hFE+3433+100k)・(470k-18k)+100k・(231・hFE+3433+hfe・18k)}
=8.2k+(104412・hFE+1551716)/(19.275・hFE+470.8)
=13.5k (hFE=300のとき)
1段目の出力と2段目の入力をつないだ際には、1段目の出力Zと2段目の入力Zで分圧されます。同様に2段目の出力と3段目の入力をつないだ際には、2段目の出力Zと3段目の入力Zで分圧されます。
この回路の出力Zは低周波ではRcに等しいので、1段目〜3段目の合成電圧増幅率Av1-3は、ゲイン(VR1)を最大にした場合、以下のように-2046倍に達します。
Av1-3=Av1・Av2・Av3・Zin2/(Zout1+Zin2)・Zin3/(Zout2+Zin3)
=-10.6・(-24.9)・(-29.8)・14.9k/(18k+14.9k)・13.5k/(10k+13.5k)
=-2046
この時、例えば2段目のトランジスタのhFEが50だったとすると、Av1-3は以下のように-1304倍にまで低下します。
上記の結果より、
∴Av2=-1/(0.0361+1.1914/hfe)
=-16.7 (hFE=50のとき)
∴Zin2=8.2k+(79580・hFE+1579k)/(10.9688・hFE+479)
=13.6k (hFE=50のとき)
∴Av1-3=Av1・Av2・Av3・Zin2/(Zout1+Zin2)・Zin3/(Zout2+Zin3)
=-10.6・(-16.7)・(-29.8)・13.6k/(18k+13.6k)・13.5k/(10k+13.5k)
=-1304
また、1〜3段目のすべてのトランジスタのhFEが100だったとすると、Av1-3は以下のように-1274倍にまで低下します。
上記の結果より、
∴Av1=-1/(0.0872+2.087/hfe)
=-9.25 (hFE=100のとき)
∴Av2=-1/(0.0361+1.1914/hfe)
=-20.8 (hFE=100のとき)
∴Av3=-1/(0.0313+0.6619/hfe)
=-26.4 (hFE=100のとき)
∴Zin1=33k+(10441k・hFE+155171k)/(1927.5・hFE+47080.1)
=38.0k (hFE=100のとき)
∴Zin2=8.2k+(79580・hFE+1579k)/(10.9688・hFE+479)
=14.2k (hFE=100のとき)
∴Zin3=8.2k+(104412・hFE+1551716)/(19.275・hFE+470.8)
=13.2k (hFE=100のとき)
∴Av1-3=Av1・Av2・Av3・Zin2/(Zout1+Zin2)・Zin3/(Zout2+Zin3)
=-9.25・(-20.8)・(-26.4)・14.2k/(18k+14.2k)・13.2k/(10k+13.2k)
=-1274
上記にて示したように、BigMuff型回路は個別トランジスタのhFEに対する素子感度が意外と高いです。よって自作する場合に所期の増幅率(使い勝手)を得るためには、使用するトランジスタのhFEによる選別を行っておく必要があるでしょう。
参考文献1:トランジスタ技術SPECIAL増刊:OPアンプによる実用回路設計(馬場 清太郎著、CQ出版社)